第1关：最长非降子序列(非连续)问题

题目

任务描述

本关任务：掌握动态规划算法思想，并能利用动态规划算法思想解决最长非降子序列（非连续）问题：

由n个正整数组成的序列，从该序列中删除若干个整数，使得剩下的整数组成单调非降子序列，求最长的单调非降子序列并输出（测试数据保证有唯一解）。

相关知识

为了完成本关任务，你需要掌握：1.动态规划的基本概念，2.动态规划的基本步骤，3.最长非降子序列求解思路。

动态规划的基本概念
动态规划(Dynamic Programming)是求解分阶段决策过程最优化问题的数学方法。动态规划算法处理的对象是多阶段决策问题的最优值。

多阶段决策问题是指这样的一类特殊的活动过程： 问题可以分解成若干相互联系的阶段，在每一个阶段都要做出决策，形成一个决策序列，该决策序列也称为一个策略。对于每一个决策序列，可以在满足问题的约束条件下用一个数值函数（即目标函数）的值来衡量该策略的优劣。多阶段决策问题的最优化目标是获取导致问题最优值的最优决策序列（最优策略），即得到最优解。

动态规划的基本步骤
根据动态规划的基本概念，可以得到动态规划的基本模型和执行步骤如下：

1. 找出最优解的性质，并刻画其结构特征：满足最优子结构性质（原问题的最优解包含着其子问题的最优解）。

2. 递归地定义最优值。

3. 以自底向上的方式计算出最优值。

4. 根据计算最优值时得到的信息，构造最优解。

最长非降子序列求解思路
n个整数序列的最长非降子序列问题可以分解成第1个整数与后n−1个整数序列的最长非降子序列的组合，是一个典型的动态规划问题。根据动态规划的基本步骤，求解思路如下：

1. 上面刚刚提到，求解n个整数序列的最长非降子序列可以转化为求解后n−1个整数序列的最长非降子序列，再与第1个进行组合，形成的序列若满足非降序列的条件，即为n个整数序列的最长非降子序列。

2. 设定n个整数序列为数组\(arr[0,1,..,n−1]\)。同时定义一个整型数组\(dp[0,1,..,n−1]\)，其中第i项（dp[i]）表示数组\(arr[i,i+1,..,n−1]\)形成的序列的最长非降子序列的长度。为了构造问题的最优解，再定义一个整型数组\(id[0,1,..,n−1]\)，其中第i项（id[i]）表示数组\(arr[i,i+1,..,n−1]\)形成的序列的最长非降子序列中，大于或等于\(arr[i]\)的下一个整数（arr[id[i]]）在数组arr中的下标。

那么最优值的定义为：
\(dp[i]=max(dp[j]+1),if(arr[i]<=arr[j]),j\in [i+1,n−1]\)
同时更新\(id[i]=j\)。

3. 根据dp和id的含义，dp数组初始化为\(dp[i]=1\)，同时id数组初始化为\(id[i]=i\)（因为每个整数至少可以用自己表示长度为1的非降子序列），为了得到全局（n个整数序列）的最优解，需要以自底向上的方式计算。

根据上述最优解转移等式，首先计算的是数组子序列\(arr[n−2,n−1]\)的最优解，再然后计算数组子序列\(arr[n−3,n−2,n−1]\)的最优解，以此类推，直到计算出数组序列\(arr[0,1,..,n−1]\)的最优解。

4. 根据上一个步骤计算最优解时得到的信息（数组dp和数组id），构造出最优解（下图绿色线条组成的序列即为最长非降子序列）。

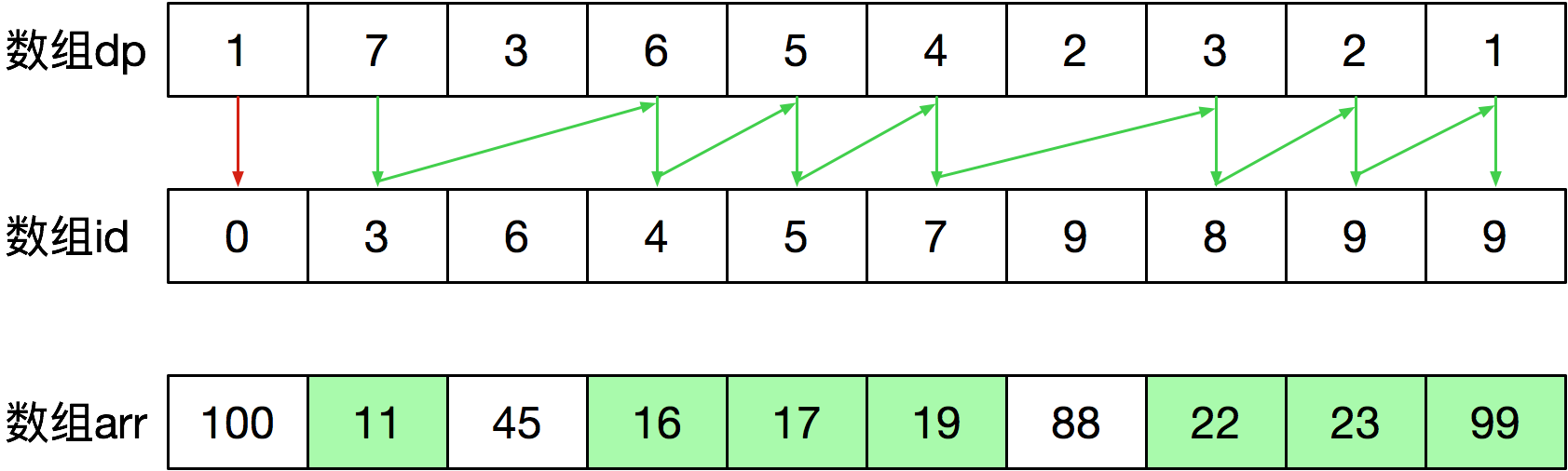
实际上，根据数组dp的信息也能构造出最优解，比如上图中，依次输出长度dp[i]为7,6,5,4,3,2,1所对应的整数。

编程要求

本关的编程任务是补全右侧代码片段main中Begin至End中间的代码，具体要求如下：

• 在main中，读取整数n以及n个整数序列，运用动态规划的算法思想编程求解出该序列的最长非降子序列，并输出（所有输出整数之间空格隔开，末尾换行）。

测试说明

平台将自动编译补全后的代码，并生成若干组测试数据，接着根据程序的输出判断程序是否正确。

以下是平台的测试样例：

测试输入：
10
100 11 45 16 17 19 88 22 23 99
预期输出：
11 16 17 19 22 23 99

参考答案

main.cpp

//
//  main.cpp
//  step1
//
//  Created by ljpc on 2018/12/8.
//  Copyright © 2018年 ljpc. All rights reserved.
//

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 101;

int main(int argc,
  const char * argv[]) {
  // 请在这里补充代码，完成本关任务
  /********* Begin *********/
  int n;
  cin >> n;
  int arr[maxn];
  memset(arr, 0, sizeof(arr));
  for (int i = 1; i <= n; i++) {
    cin >> arr[i];
  }
  int id[maxn];
  memset(id, 0, sizeof(id));
  int dp[maxn];
  for (int i = 1; i <= n; i++) dp[i] = 1;
  int max_index = 0;
  int ans = 1;
  for (int i = n - 1; i >= 1; i--) {
    for (int j = i + 1; j <= n; j++) {
      if (arr[i] < arr[j] && dp[j] + 1 > dp[i]) {
        dp[i] = dp[j] + 1;
        id[i] = j;
      }
    }
    if (dp[i] > ans) {
      max_index = i;
      ans = dp[i];
    }
  }
  int i = max_index;
  cout << arr[i] << " ";
  while (id[i]) {
    i = id[i];
    cout << arr[i] << " ";
  }
  cout << endl;
  /********* End *********/
  return 0;
}