第1关：n位逐位整除数

题目

任务描述

本关任务：掌握回溯法算法思想，并能利用回溯法算法思想解决n位逐位整除数问题。

n位逐位整除数（简称整除数）：从其高位开始，高1位能被整数1整除（显然），高2位能被整数2整除，…，整个n位能被整数n整除。给定整数n，求所有的n位整除数的个数。

例如，整数102450就是一个6位整除数。

相关知识

为了完成本关任务，你需要掌握：1.回溯法的基本思想，2.回溯法的基本步骤，3.回溯法的算法框架，4.整除数的求解思路。

回溯法的基本思想
有许多问题，当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。

回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。

回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果包含，进入该子树，继续按深度优先策略搜索。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯。

回溯法的基本步骤
根据回溯法的基本思想，可以得到回溯法的基本步骤如下：

针对所给问题，定义问题的解空间；
确定易于搜索的解空间结构；
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。
其中，两个常用的剪枝函数为：

约数函数：在扩展结点处减去不满足约束的子树 ；
限界函数：减去得不到最优解的子树。
对于问题的一个实例，解向量满足显式约束条件的所有多元组，构成了该实例的一个解空间：

问题的解向量：回溯法希望一个问题的解能够表示成一个n元式\((x_1,x_2,..,x_n)\)的形式；

显约束：对分量\(x_i\)的取值限定；

隐约束：为满足问题的解而对不同分量之间施加的约束（通常用于剪枝）。

回溯法的算法框架
回溯法对解空间树作深度优先搜索，因此，在一般情况下用递归方法实现回溯法。具体算法框架及其伪代码如下：

void backt\frack (int t)//按深度优先从t层推进到第t+1层
{
    if (t > n){
        output (x); // 到达叶子结点，将计算或结果输出
    }
    else {
        for (int i = f(n,t); i <= g(n,t); i ++ ){// 遍历结点t的所有子结点
            x[t] = h[i];
            if (constraint (t) && bound (t)){
                backt\frack (t + 1);//如果不满足剪枝条件继续遍历
            }
            //回溯到该层的其他结点，然后继续搜索解空间
        }
    }
}

整除数的求解思路
n位整除数的解法可以暴力枚举每一位数字，然后通过试除法进行验证，显然，这样的方法复杂度非常高，而且非常多的无效组合。运用回溯法算法可以很好的避免无效的组合，提高检索效率。根据回溯法的基本步骤，可得到如下回溯解法：

针对n位整除数问题，它的解空间为：第1位可能的数字为1,2,..9，第2至第n位可能的数字都为0,1,..9，因此共\(9×10^{(n−1)}\)个可能的解；

解空间结构：用数组a[1,2,..n]表示整除数问题的一个解，其中a[1]!=0，求解时按索引t=1开始，依次递归得到数组a；

以深度优先的方式搜索解空间，若当前的整数a[1,2,..t]不能整除整数t，则剪枝。

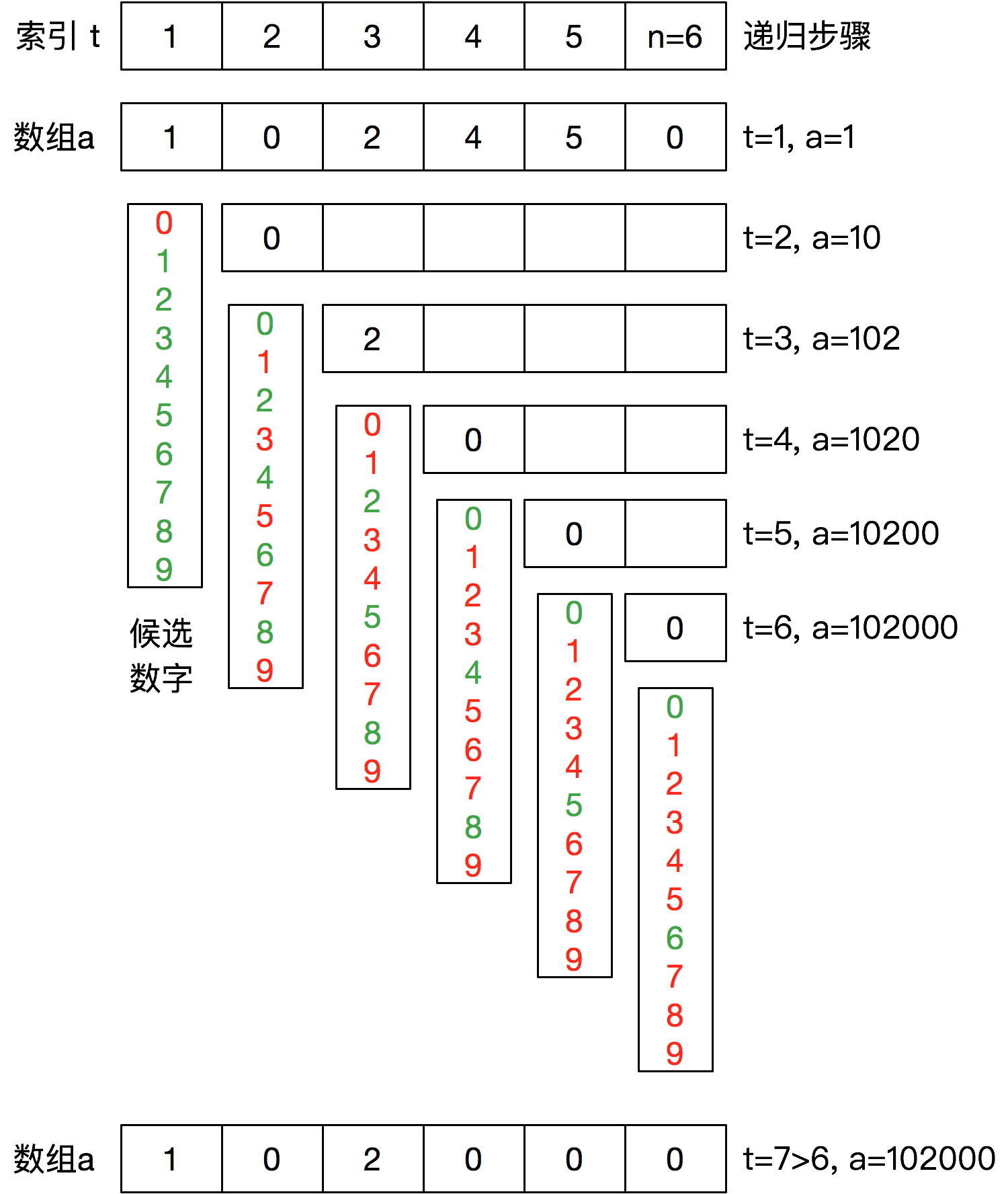
例如n=6时，回溯法的过程如下图所示。t=1，候选数字为0,1,2,..9，其中0是不符合整数第1位不为0的规则，设置当前的数字为a[t=1]=1；递归，t=t+1=2，数字0,2,4,6,8与a[1]所组合的整数a[1,2]是能被t=2整除的，设置当前的数字为a[t=2]=0；以此类推，直到t=7时，超过了指定的长度n=6，当前递归搜索结束，整除数个数加1。然后回溯到t=6时其它的合法数字，继续递归搜索。再然后回溯到t=5时其他的合法数字，继续递归搜索。以此类推，完成整个解空间的搜索。
​

编程要求

本关的编程任务是补全右侧代码片段backt\frack中Begin至End中间的代码，具体要求如下：

在backt\frack中，根据回溯法算法的思想，遍历和统计n位逐位整除数的个数。 其中，参数数组a记录满足条件的整除数（整除数长度n超过int64位存储范围，所以用整型数组模拟存储），参数t（初始为1）表示当前整除数长度（t<=n），参数n表示待查询的整除数长度，取地址引用的参数sum表示整除数的个数。

测试说明

平台将自动编译补全后的代码，并生成若干组测试数据，接着根据程序的输出判断程序是否正确。

以下是平台的测试样例：

测试输入：6
预期输出：1200

开始你的任务吧，祝你成功！

参考答案

main.cpp

//
//  main.cpp
//  step1
//
//  Created by ljpc on 2018/12/8.
//  Copyright © 2018年 ljpc. All rights reserved.
//

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;


void backtrack(int *a, int t, int n, int &sum)
{
    // 请在这里补充代码，完成本关任务
    /********* Begin *********/
    if(t==n+1){
        int y=0,m=0;
        for(int i=0;i<n;i++){
            y=(m*10+a[i])%n;
            m=y;
        }
        if(y==0){
            sum++;
        }
    }
    else{
        if(t==1){
            for(int i=1;i<10;i++){
                a[t-1]=i;
                backtrack(a, t+1, n, sum);
            }
        }
        else{
            int y=0,m=0;
            for(int i=0;i<t-1;i++){
                y=(m*10+a[i])%(t-1);
                m=y;
            }
            if(y==0){  
	            for(int i=0;i<10;i++){
	                a[t-1]=i;
	                backtrack(a,t+1,n,sum);
	            }
	        }
        }
    }
    /********* End *********/
}


int main(int argc, const char * argv[]) {
    
    int a[101];
    int n;
    scanf("%d", &n);
    
    int sum = 0;
    backtrack(a, 1, n, sum);

    printf("%d\n", sum);
    
    return 0;
}